재미난 DP 문제입니다.

문제

BOJ 19545 소가 길을 건너간 이유 2020

$N, M$개의 정점이 있는 이분 그래프에 $N+M-1$개의 간선을 배치하여 모든 정점 간의 거리의 합이 최소가 되도록 하는 문제입니다. 이때 연결그래프여야 하며, 간선끼리 겹치면 안된다는 조건이 있으므로 특수한 형태의 그래프만 가능합니다.

분석

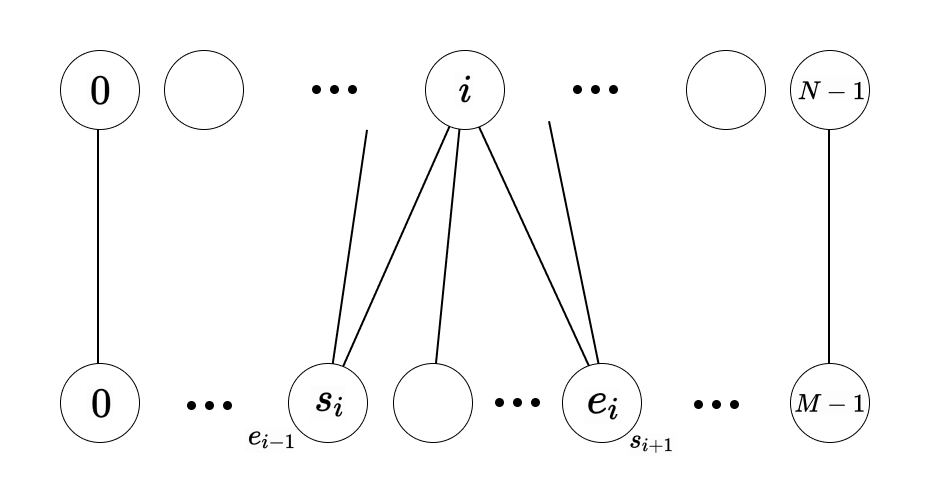
graph

위의 정점에서 아래의 정점으로 간선을 잇는다고 생각하면 연속한 구간의 정점들에 연결되어야 하며, 구간끼리는 양끝점이 겹쳐야 합니다. 다시 말해, 위의 $i$번 정점에서 아래의 $s_i$부터 $e_i$까지 간선을 만든다면 아래의 조건을 만족해야 합니다.

\[e_i=s_{i+1} \, (0 \leq i < N-1)\] \[s_0 = 0, \, e_{N-1} = M-1\]

위의 $i$번 정점과 아래의 $j$번 정점 간에 간선을 만든다면 가중치(거리)는 아래와 같이 구할 수 있습니다.

\[dis_{i, j}=(U_i - D_j)^2 + L^2\]

위의 $i$번 정점은 아래의 $s_i$부터 $e_i$까지 간선을 만드므로 아래의 $j$는 $(s_i \leq j \leq e_i)$입니다. 모든 정점들 간의 거리의 합을 최소화해야 하므로, 각각의 정점이 사용되는 횟수를 간선의 가중치와 곱해 거리의 합을 구할 수 있습니다.
그래프를 그려서 계산해보면, 위의 $i$번 정점과 아래의 $j$번 정점이 연결될 때 추가되는 거리는 다음과 같습니다.

\[C_{i, j} = \begin{cases} f(i, j) = dis_{i, j} \cdot (i + j + 1)(M + N - i - j - 1) & \text{$j=s_i$ or $j=e_i$} \\ g(i, j) = dis_{i, j} \cdot (M + N - 1) & \text{$s_i < j < e_i$} \\ \end{cases}\]

이제 아래 $M$개의 정점을 $N$개의 구간 $(s_0, e_0),…,(s_{N-1}, e_{N-1}) $으로 나눠 $C_{i, j}$의 합이 최소가 되도록 하면 됩니다.

풀이

$dp_{i, j}$를 위 $i$번 정점까지, 아래 $j$번 정점까지 조건(연결그래프이며 겹치는 간선은 없다)을 만족하며, 위의 $i$번 정점과 아래 $j$번 정점을 연결했을 때 거리의 합의 최솟값으로 정의합니다. $i$를 $0$부터 $N-1$까지 증가시키며 모든 $j$에 대해 $dp_{i, j}$를 계산합니다. 이때 값은 아래와 같이 전이됩니다.

\[dp_{i, j} = \min\limits_{k \leq j} \Big(dp_{i-1, k} + \sum\limits_{l=k}^{j} C_{i, l} \Big)\]

위의 $i$번 정점은 아래의 $(s_i, e_i)=(k, j)$ 의 구간에 간선을 연결하게 됩니다. 이때의 시간 복잡도는 $O(N M^2)$ 이므로 추가적인 아이디어가 필요합니다.

최적화

$C_{i, l}$이 구간의 양끝에 있는 경우 $\text{$l=k$ or $l=j$}$ 에는 $f(i, l)$로 다르게 계산하므로 까다롭습니다.
하지만 원래 구간의 길이가 $2$ 이상이라면 구간의 왼쪽은 고정하고 오른쪽만 $1$ 늘리는 것은 어렵지 않습니다. 즉, 구간 $(k, j-1)$ 이 구간 $(k, j)$가 된다면 $f(i, j) - f(i, j - 1) + g(i, j - 1)$을 더해주어 쉽게 구할 수 있습니다.
따라서 $dp_{i, j}$를 업데이트할 때, $j-1$ 까지 마지막 구간의 길이가 $2$ 이상인 경우의 최솟값을 관리하면 더 빠르게 할 수 있습니다.

\[c_1=dv- f(i, j - 1) + g(i, j - 1) + f(i, j) \\ c_2=f(i, j-1) + f(i, j) + dp_{i-1, j-1}\\ c_3=g(i, j) + dp_{i-1, j} \\ dp_{i, j} = min(c_1, c_2, c_3), dv = min(dv, c_1, c_2)\]

$dv$는 마지막 구간의 길이가 $2$ 이상인 경우의 최솟값입니다. $c_1$은 $dv$의 구간을 $1$ 늘리므로 구간의 길이가 $3$ 이상인 경우, $c_2$는 구간의 길이가 $2$, $c_3$은 $1$인 경우입니다. $dp_{i, j}$ 를 업데이트할 때는 구간의 길이에 따라 세 가지 경우 중 최솟값이 됩니다. 이 과정을 통해 시간복잡도를 $O(NM)$으로 줄일 수 있습니다. 아래는 위의 내용을 구현한 코드입니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll cache[3000];

ll N, M, L;
ll U[3000], D[3000];
ll dis[3000][3000];
const ll MAX = 1e17;

ll f(ll i, ll j) { return dis[i][j] * (i + j + 1) * (M + N - i - j - 1); }

void solve() {
  cin >> N >> M >> L;
  for (int i = 0; i < N; ++i) cin >> U[i];
  for (int i = 0; i < M; ++i) cin >> D[i];
  for (int i = 0; i < N; ++i) for (int j = 0; j < M; ++j) {
    dis[i][j] = (U[i] - D[j]) * (U[i] - D[j]) + L * L;
  }
  for (int i = 0; i < M; ++i) cache[i] = MAX;
  cache[0] = 0;
  ll ncache[3000];
  for (int i = 0; i < N; ++i) {
    ll dv = MAX;
    for (int j = 0; j < M; ++j) {
      ll c1, c2, c3;
      if (j != 0) c1 = dv - f(i, j - 1) + dis[i][j - 1] * (M + N - 1) + f(i, j);
      else c1 = MAX;
			
      if (j != 0) c2 = f(i, j - 1) + f(i, j) + cache[j - 1];
      else c2 = MAX;
			
      c3 = cache[j] + dis[i][j] * (M + N - 1);

      ncache[j] = min({c1, c2, c3});
      dv = min(c1, c2);
    }
    swap(ncache, cache);
  }
  cout << cache[M - 1];
}

int main() {
  ios::sync_with_stdio(0); cin.tie(0);
  solve();
}

정해는 격자판에서의 경로로 변환하여 풀이하며 상당히 아름답습니다. 사실 구간을 관리하는 것과 동일하다는 것을 알 수 있습니다. 저는 마지막 구간의 길이가 $2$ 이상인 경우를 관리하는 괴상한(?) 방법으로 최적화하였지만, 정해는 격자판에서 이동하는 방향을 dp에 포함합니다. 정해와 다른 풀이라 글을 작성하였는데, 정해도 읽어보시는 것을 추천드립니다.